アームの運動学

　　余弦定理について再学習

plotclockのプログラムにも使われている余弦定理を確認しておきます。

１．余弦定理

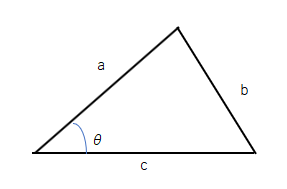
図の三角形において、次の式が成り立つ。 \[b^{2}=a^{2}+c^{2}-2ac\cos\theta\] これにより、\(\theta\)は、 \[\theta=\cos^{-1}(\frac{a^{2}+c^{2}-b^{2}}{2ac})\]

２．余弦定理の導き方

図の三角形において、
\(\triangle\mathrm{ABH}\)で
\(\cos\theta= \dfrac{BH}{a}\)　　　\(\sin\theta=\dfrac{AH}{a}\)　より
\(BH=a* \cos\theta\)　　　\(AH=a* \sin\theta\)
\(\triangle\mathrm{AHC}\)で
\begin{align} b^{2} &= AH^{2}+HC^{2}\\ &= (a*\sin\theta)^{2}+(c-a*\cos\theta)^{2}\\ &= a^{2}\sin^{2}\theta+c^{2}-2ac\cos\theta+a^{2}\cos^{2}\theta\\ &= a^{2}(\sin^{2}\theta+\cos^{2}\theta)+c^{2}-2ac\cos\theta \end{align} \(\sin^{2}\theta+\cos^{2}\theta=1\) により
\[b^{2} =a^{2}+c^{2}-2ac\cos\theta\] \[\theta=\cos^{-1}(\frac{a^{2}+c^{2}-b^{2}}{2ac})\]

３．「plotclock」のプログラムに使われている余弦定理
　次の個所で使われています。

					
double return_angle(double a, double b, double c) {

  return acos((a * a + c * c - b * b) / (2 * a * c));

}						

　三角関数について、数学上では、\(\sin,\ \cos,\ \tan\)の逆関数はそれぞれ \(\sin^{-1},\ \cos^{-1},\ \tan^{-1}\)で表記しますが、
プログラムでは、逆関数の表記は、asin、acos、atanで表記します。

　また、atanとatan2の違いは、
＊atan(y/x)は、tanθ=y/x となるθを求める表記で、 θ= atan(y/x)　(x>0, -π/2<θ<π/2)です。
＊atan2（x, y)は、デカルト座標における(x, y)の偏角を求める表記で、 θ= atan2（y, x）　( -π<θ<π)です。

　プログラム言語によっては、atan2（x, y)と表記するものがあります。

２つの関係は、x>0のとき、atan(y/x) = atan2(y, x)です。

　　2リンクモデルの一般的な運動学

　「AGI Robotsさんのkinematics 運動学入門」の記事を参考にさせていただきました。
下図のような2つのリンク（Link）がそれぞれ「joint」で接続された2リンクモデルを用いて運動学を学習します。

　

　「ジョイントの変位」は「joint 1」と「joint 2」の角度 \(\theta_{1}\)と \(\theta_{2}\)です。
また、「アームの位置や姿勢」はリンク２の手先の位置の \((x, y)\)です。各リンクの長さはそれぞれL1とL2として考えます。
ジョイントの変位である各関節角度 \(\theta_{1}\)と \(\theta_{2}\)を用いて、アームの位置である手先の 位置 \((x, y)\)を数式で表します。

１．リンク１について
　原点にある joint 1とリンク１より、原点からリンク１の先の joint 2の位置 \((x_{1}, y_{1})\)は、 \[x_{1} = L_{1} \cos \theta_{1}\] \[y_{1} = L_{1} \sin \theta_{1}\] と三角関数を用いて求められます。


２．リンク２について
　joint 2を基準としたときのリンク２の先の位置 \((x_{2}, y_{2})\)を求めます。
　リンク２の角度は、Joint 2に加えてJoint 1の角度も影響します。

　リンク２の角度 \(\theta\)は、 \[\theta = \theta_{1}+\theta_{2}\] となります。
　したがってjoint 2の位置を基準とした時のリンク２の先の位置 \((x_{2}, y_{2})\)は、 \[x_{2}=L_{2}(\cos(\theta_{1}+\theta_{2})\] \[y_{2}=L_{2}(\sin(\theta_{1}+\theta_{2})\] のようになります。


３．モデル全体について
　原点を基準としたアームの手先の位置 \((x, y)\)を求めます。
アームの位置は、これまでに求めた２つのリンクや回転関節を用いて求めた距離を合わせで求められるため、 \[ \begin{cases} x&=x_{1}+x_{2}=L_{1}\cos\theta_{1}+L_{2}\cos(\theta_{1}+\theta_{2})\\ y&=y_{1}+y_{2}=L_{1}\sin\theta_{1}+L_{2}\sin(\theta_{1}+\theta_{2}) \end{cases} \] となります。


４．逆の式について
　上記の「アームの先の位置 \((x, y)\)」から関節の変位\(\theta_{1}\)と\(\theta_{2}\)を表す数式を求めます。
上記の式より、 \[x-L_{1}\cos(\theta_{1})=L_{2}\cos(\theta_{1}+\theta_{2})\] \[y-L_{1}\sin(\theta_{1})=L_{2}\sin(\theta_{1}+\theta_{2})\] この2つの式の両辺を2乗すると、 \[x^{2}-2xL_{1}\cos(\theta_{1})+L_{1}^{2}\cos^{2}(\theta_{1})=L_{2}^{2}\cos^{2}(\theta_{1}+\theta_{2})\] \[y^{2}-2yL_{1}\sin(\theta_{1})+L_{1}^{2}\sin^{2}(\theta_{1})=L_{2}^{2}\sin^{2}(\theta_{1}+\theta_{2})\] 次に、2つの式の両辺をそれぞれ足すと、 \[x^{2}+y^{2}-2xL_{1}\cos(\theta_{1})-2yL_{1}\sin(\theta_{1})+L_{1}^{2}\cos^{2}(\theta_{1})+L_{1}^{2}\sin^{2}(\theta_{1})\] \[=L_{2}^{2}\cos^{2}(\theta_{1}+\theta_{2})+L_{2}^{2}\sin^{2}(\theta_{1}+\theta_{2})\] \[x^{2}+y^{2}-2L_{1}(x\cos(\theta_{1})+y\sin(\theta_{1}))+L_{1}^{2}(\cos^{2}(\theta_{1})+\sin^{2}(\theta_{1}))\] \[=L_{2}^{2}(\cos^{2}(\theta_{1}+\theta_{2})+\sin^2(\theta_{1}+\theta_{2}))\] \[x^{2}+y^{2}-2L_{1}(x\cos(\theta_{1})+y\sin(\theta_{1}))+L_{1}^{2}=L_{2}^{2}\] この式を\(\theta_{1}\)について解きます。、 \[2L_{1}(x\cos(\theta_{1})+y\sin(\theta_{1}))=x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}\] \[x\cos(\theta_{1})+y\sin(\theta_{1})=\dfrac{x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}}{2L_{1}}\] ここで、三角関数における \[a\cos(x)+b\sin(x)=\sqrt{a^{2}+b^{2}}\cos(x-\tan^{-1}(\dfrac{b}{a}))\] を使って, \[\sqrt{x^{2}+y^{2}}\cos\left(\theta_{1}-\tan^{-1}\left(\dfrac{y}{x}\right)\right)=\dfrac{x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}}{2L_{1}}\] この式を\(\theta_{1}\)について解くと, \[\cos\left(\theta_{1}-\tan^{-1}\left(\dfrac{y}{x}\right)\right)=\dfrac{x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}}{2L_{1}\sqrt{x^{2}+y^{2}}}\] \[\theta_{1}-\tan^{-1}\left(\dfrac{y}{x}\right)=\pm\cos^{-1}\left(\dfrac{x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}}{2L_{1}\sqrt{x^{2}+y^{2}}}\right)\] \[\theta_{1}=\tan^{-1}\left(\dfrac{y}{x}\right)\pm\cos^{-1}\left(\dfrac{x^{2}+y^{2}+L_{1}^{2}-L_{2}^{2}}{2L_{1}\sqrt{x^{2}+y^{2}}}\right)\] となり、\(\theta_{1}\)に関する式を求めることが出来ました。

５．θ2について
　同様に、\(\theta_{2}\)についての式を求めていきます。 \[x-L_{1}\cos(\theta_{1})=L_{2}\cos(\theta_{1}+\theta_{2})\] \[y-L_{1}\sin(\theta_{1})=L_{2}\sin(\theta_{1}+\theta_{2})\] より、2つ目の式を1つ目の式で割ると, \[\dfrac{y-L_{1}\sin(\theta_{1})}{x-L_{1}\cos(\theta_{1})}=\dfrac{L_{2}\sin(\theta_{1}+\theta_{2})}{L_{2}\cos(\theta_{1}+\theta_{2})}\] 右辺を変換すると、 \[\dfrac{L_{2}\sin(\theta_{1}+\theta_{2})}{L_{2}\cos(\theta_{1}+\theta_{2})}=\tan(\theta_{1}+\theta_{2})\] となるので、 \[\tan(\theta_{1}+\theta_{2})=\dfrac{y-L_{1}\sin(\theta_{1})}{x-L_{1}\cos(\theta_{1})}\] 　となります。
この式を \(\theta_{2}\)について解くと、 \[\tan(\theta_{1}+\theta_{2})=\dfrac{y-L_{1}\sin(\theta_{1})}{x-L_{1}\cos(\theta_{1})}\] \[\theta_{1}+\theta_{2}=\tan^{-1}\left(\dfrac{y-L_{1}\sin(\theta_{1})}{x-L_{1}\cos(\theta_{1})}\right)\] \[\theta_{2}=\tan^{-1}\left(\dfrac{y-L_{1}\sin(\theta_{1})}{x-L_{1}\cos(\theta_{1})}\right)-\theta_{1}\] のように、\(\theta_{2}\)に関する式を求めることが出来ました。

　　plotclockプログラムの確認

　plotclockプログラム中の「void set_XY( )」について確認しておきます。
記述に誤謬がある場合も有りますので、その時は申し訳ありません。

１．void set_XY()のプログラムは、次のようになっています。分かり易くするために多少変更しています。

void set_XY(double Tx, double Ty)
{
  double dx, dy, c, a1, a2, a3, a4, a5, a6, Hx, Hy;
  dx = Tx - O1X;
  dy = Ty - O1Y;
  
  c = sqrt(dx * dx + dy * dy);
  a1 = atan2(dy, dx);
  a2 = return_angle(L1, L2, c);
  servo2.writeMicroseconds(floor(((a2 + a1 - M_PI) * SERVOFAKTORLEFT) + SERVOLEFTNULL));

  a3 = return_angle(L2, L1, c);
  a5 = (a1-a3+angle_of_JoinerArm)-M_PI);
  
  Hx = Tx + L3 * cos(a5);
  Hy = Ty + L3 * sin(a5);
  dx = Hx - O2X;
  dy = Hy - O2Y;
  
  c = sqrt(dx * dx + dy * dy);
  a6 = atan2(dy, dx);
  a4 = return_angle(L1, L4, c);
  servo3.writeMicroseconds(floor(((a6 - a4) * SERVOFAKTORRIGHT) + SERVORIGHTNULL));
}
						

２．ペンとサーボ左関節と腕関節の間の三角形を計算します。
　アームの図は次の通りです。


（１）左サーボについては、次の図のようになります。
　角度の値はすべてラジアンです。

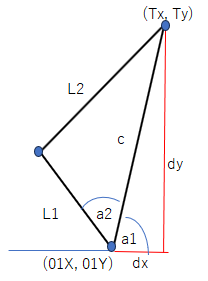
\(dx=Tx-O1X\)
\(dy=Ty-O1Y\)

\(c=\sqrt{dx^{2}+dy^{2}}\)

\(a_{1}=atan2(dy, dx)\)

\(a_{2}=acos(\dfrac{L_{1}^{2}+c^{2}-L_{2}^{2}}{2L_{1}c})\)

　この \(a_{2}\) は、プログラムでは
a2 = return_angle(L1, L2, c)となっています。

したがって左サーボの可動は、
servo2.writeMicroseconds(floor(((a2 + a1 - M_PI) * SERVOFAKTORLEFT) + SERVOLEFTNULL))

となります。

（２）次に左腕の位置に基づいてペン関節の位置を図にしたがって計算します。


　余弦定理から、 　　　\(a_{3} =\) return_angle\((L_{2}, L_{1}, c)\)
　　　\(a = a_{1}-a_{3}\)
　　　\(a_{5}=a+b=a_{1}-a_{3}+b\)

　　　\(\angle b\) の値を\(angleOfJoinerArm\)とすると、
　　　\(a_{5}=(a_{1}-a_{3}+angleOfJoinerArm)-\pi\)
として、
　　　\(H_{x}=T_{x}+\cos(a_{5})\)
　　　\(H_{y}=T_{y}+\sin(a_{5})\)
（Hx、Hyはペンジョイントの位置です。）

　ここで \(angleOfJoinerArm\) は固定されており、図より

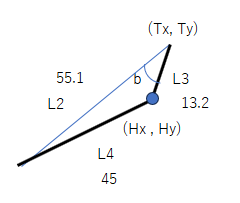
　　\(angleOfJoinerArm=acos(\dfrac{L_{2}^{2}+L_{3}^{2}-L_{4}^{2}}{2L_{2}L_{3}})\)
　　\(L2=55.1,\ \ L3=13.2,\ \ L4=45\) としているので、

　　\(\dfrac{L_{2}^{2}+L_{3}^{2}-L_{4}^{2}}{2L_{2}L_{3}}=\dfrac{3036.01+174.24-2025}{1454.64}\)
　　\(=0.8148\)

したがって、 　　\(AngleOfJoinerArm=acos(0.8148)=0.6184 //（=35,4°\)）

３．次にペンジョイント、右サーボ、アームジョイントの間の三角形を計算します。
　右サーボの図にしたがって計算すると、

　　\(d_{x}=H_{x}-O2X\)
　　\(d_{y}=H_{y}-O2Y\)
より
　　\(c=\sqrt{dx^{2}+dy^{2}}\)


　　\(a_{6}=atan2(d_{y},\ d_{x})\)
　　\(a_{4}=\)return_angle\((L_{1},\ L_{4},\ c)\)

よって右サーボの可動は、
\(servo3.writeMicroseconds(floor(((a6 - a4) * SERVOFAKTORRIGHT) + SERVORIGHTNULL))\)
となります。